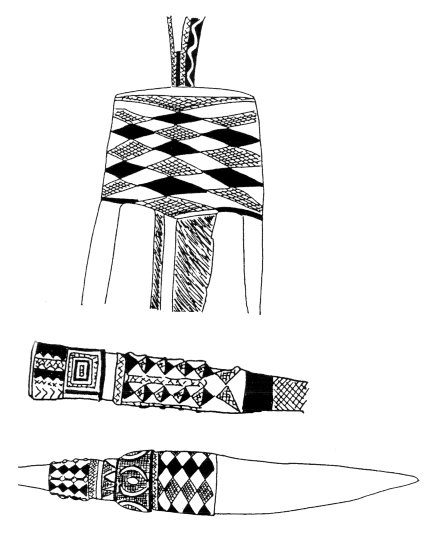
|
Donald W. Crowe
Abstract
1. Introduction In some sense the application of mathematics (geometry, in this case) which will be discussed here, in an informal way, begins with the Swiss group theorist, Andreas Speiser. The 1927 (second) edition of Speiser's pioneering group theory text [13] appeared as volume 5 of the famed Springer "yellow peril" series of books whose general title was "The Fundamental Principles of the Mathematical Sciences in Individual Treatises With Special Attention to Their Applications". The subtitle of Speiser's book declares its applications to be the algebraic numbers and crystallography. However, he devotes an entire chapter to Symmetry of Ornaments (by "ornament" he generally means what I will refer to as "repeated pattern" in this paper). The contents of that chapter implicitly lead to the possible applications to anthropology and archaeology to which the present article is an informal introduction. Speiser's own emphasis in his Symmetry of Ornaments chapter was on the repeated patterns found in the tombs of ancient Egypt. He considered the analysis of the group theoretic structure of the symmetries of such plane patterns to be the simplest introduction to the (for him) most significant application of group theory, the crystallographic groups, i.e. the groups of symmetries of space patterns. But besides that, the creation of these patterns was a hitherto neglected part of the history of mathematics, the "prehistory of group theory", which has a continuous history, via these patterns, to the present time. He quotes the prominent Egyptologist, Flinders Petrie, as writing "Practically it is very difficult, or almost impossible, to point out decoration which is proved to have originated independently, and not to have been copied from Egyptian stock". The finite groups of symmetries
of space are illustrated by the five regular polyhedra which were carefully
constructed by Euclid in "The Elements", and were seen by Plato to be essential
to the basic structure of the universe. In the view of some these remarkable
Greek contributions represent the beginnings of higher mathematics. But,
says Speiser, the discovery of the infinite groups of symmetries of the
plane, as illustrated by the Egyptian patterns, pushes back the beginnings
of higher mathematics some 1,000 years further than previously recognized,
to about 1500 BC. Moreover, he says, the discovery of the particular quite
complicated group (now called p4g) of the pattern shown in Figure
1 "is certainly a mathematical achievement of the first rank"1.
Figure 1: The
ancient Egyptian pattern described by Speiser as being a mathematical
But we want to shift the emphasis on the analysis of patterns from history of mathematics to cultural studies. This process was begun with the publication of Edith Mueller's 1944 PhD thesis [11], which gave a detailed mathematical analysis of the Moorish ornaments in the Alhambra. Most of us consider this to be the mathematical beginning of the cultural study of repeated patterns, though in American archaeology similar ideas were introduced by George Brainerd in 1942 [1] and in more detail by Anna Shepard in 1948 [12]. I will return in a later section to the interesting story of Edith Mueller. My own interest in the possible use of patterns as a tool for the study of cultural relationships came after I was exposed to the use of linguistic tools. A colleague in Nigeria came to the mathematics department to explain how linguists tried to use comparative word lists to determine how much time had elapsed since two somewhat similar languages had diverged. At that time there was a popular view among the Yoruba that they were descended from the ancient Egyptians and had in fact migrated in some not too distant past from Egypt to their present location in southwest Nigeria. This colleague had compared lists of some 100 names of basic objects in the two languages and plugged the numbers of overlapping words into a standard linguistic formula to come out with 300 years as the elapsed time since the two languages diverged. This seemed rather too short a time, and it turned out that he was not very adept at the use of logarithms and had misplaced a decimal. But the idea stuck in my mind and when I read Speiser's book and looked more carefully at Edith Mueller's thesis it seemed to me that a comparison of patterns, perhaps by their presence or absence, or by the frequency of their occurrence, might give information about relations between cultures which were neighbors either in space or in time. The first step in this process was to
learn how to classify repeated patterns. This had been done by the crystallographers
for space patterns in the 19th Century, and Pó1ya had
shown that their results included the necessary information for plane patterns,
which was the same information contained in Speiser's text and applied
by Mueller to the Alhambra decorations. So next I needed to find some graduate
students who would do similar analysis of a variety of African cultures.
But, alas, in those days there were no "Art and Mathematics" conferences,
and no "Bridges" conferences and no interest in such interdisciplinary
activity. Even when I received a small grant to hire a student assistant
I could find no takers at the University of Wisconsin. Not until Claudia
Zaslavsky asked me for some help with her book Africa Counts [15]
did I realize I would have to do it myself. Eventually I met Dorothy Washburn,
who had realized on her own that for her study of Anasazi pottery a sound
mathematical method was needed, and had reconstructed much of the crystallographic
classification for that purpose. Together we prepared a handbook, Symmetries
of Culture [14], for the use of anthropologists
and archaeologists. The next section will describe this pattern classification
tool, and mention some of the cultural phenomena to which it has been applied.
The final section will report on two small field trips to Fiji and Tonga
and the nature of the "two-color" patterns found there and in the Admiralty
Islands.
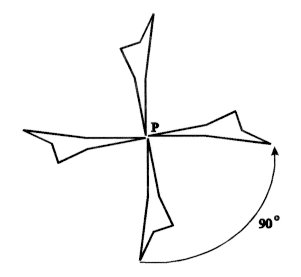
2. Geometric Principles 2.1 The four rigid motions of the Euclidean plane onto itself. The basic tool for the study and creation of repeated patterns is symmetry. Synonyms are rigid motion and isometry, which are often used to emphasize the defining property of symmetry, which is that symmetry is a distance-preserving transformation of the plane onto itself Familiar examples are rotation about a given point by a given angle, translation in a given direction by a given distance, and reflection in a given line. Some specific examples: Rotation:
If we take a flat sheet of paper lying on a desk, stick a pin through some
point of the paper and turn the whole sheet around the pin, by a quarter-
turn (90o) around the pinned point, we have performed a "rotation
by 90o about the point
P", illustrated in Figure
2. (Here
P denotes the point on the paper pierced by the pin.)
Of course the sheet of paper is not the whole plane in which it lies, but
it is customary to think of it as representing the whole plane. Throughout
our discussion it will be noticed that we are talking about a plane which
extends to infinity in all directions, even though the practical application
of the ideas is always to a finite piece (such as the sheet of paper, or
a weaving sample on a loom) of its infinite plane.
Figure 2: Rotation by 90o about point P. Translation: Suppose a flat sheet of paper (the plane) lies on a desk top, with one edge along the edge of the desk. Then suppose the paper is pushed directly away from you, so that its edge is now three inches away, but still parallel to the edge of the desk. This operation is a translation by distance 3" in a direction perpendicular to the edge of the desk. In the language of vectors, the vector which describes this translation has length 3" and direction perpendicular to the edge of the desk. There is an exact correspondence between vectors and translations: every vector in a plane defines a unique translation, and every translation of a plane onto itself can be described by some vector in that plane. See Figure 3 for a reminder that rehanging a picture on a wall generally represents a translation of the picture.
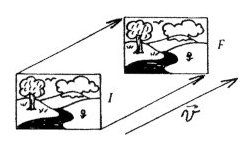
Figure 3: Translation by vector v. Reflection: If a straight line is drawn on a piece of paper (the plane again) and the paper is folded along this line then every point P on one side of the line lies against some point P' on the other side of the line. The transformation which takes each point P to its corresponding point P' is a reflection in the line. The name is explained by the fact that if a straight-edged mirror is placed along the line, perpendicular to the plane of the paper, then the apparent position of P in the mirror is the point P' just described. Another description of the relation between points P and their images P' is that if a perpendicular segment is dropped from P to the line on the (unfolded) paper and then extended the same distance on the other side of the line, the end of the extended segment is P'. Figure 4 shows the reflection of three points A,B,C in a line l to their three images A',B',C'. (Note that the term rigid motion can sometimes be slightly misleading, since the isometries which reverse orientation - such as reflection - cannot actually be carried out on a physical figure without lifting it out of its plane, in contrast to rotation and translation which can be performed without lifting the figure from its plane.)
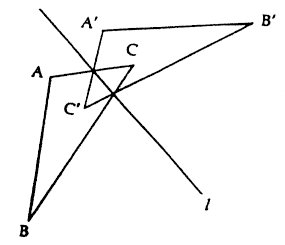
Figure 4: Reflection in line l. There is another less familiar symmetry, which is easy to describe, but in practice usually more difficult to recognize. It is Glide reflection: If every point P in the plane is translated by a given vector v and then reflected in a line l parallel to v to point P' the transformation taking P to P' is called a glide reflection, and the line l is the axis of the glide reflection. The footprints in Figure 5 are intended to suggest glide reflection. Each foot on one side of the line is translated by vector v and then reflected to the next foot on the other side of the line. A two-dimensional version of this is shown in Figure 6, where two horizontal glide axes are marked as dashed lines. 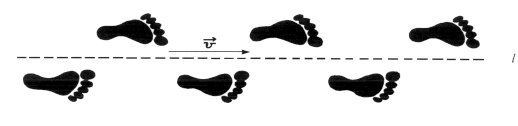
Figure 5: Glide reflection in a one-dimensional pattern.
Figure 6: Glide reflection in a two-dimensional pattern. It may seem that it is redundant to introduce the idea of a glide reflection, since it is a combination of two of the other isometrics. However, even though we do not ordinarily think of it in this way, translations and rotations are themeselves combinations of (two) reflections. Indeed, it is a fundamental fact that the reflections are the building blocks from which all isometries are constructed. However, this superficial analogy to prime numbers as the building blocks of all numbers is far from accurate. For one, no isometry is uniquely represented as a combination of reflections, and, in contrast to the fact that there is no upper bound to the number of prime factors a number may have, no more than three reflections are ever needed to represent any given isometry. This latter fact, that "every isometry is a combination of (three or fewer) reflections", is the essential step in a proof of the following fundamental Theorem: Every rigid motion (i.e. isometry) of the plane onto itself, no matter how complicated it may seem, is one of the four described above. That is, every rigid motion is either a rotation, translation, reflection or glide reflection. (In interpreting this theorem, note that "rigid motion" involves only the initial position and the final position of the points of the plane. For example the translation which takes the framed painting in Figure 3 to its new position is defined by the original position and the new position alone. Any intermediate activity, such as placing the painting on the floor while deciding where it should go, is not part of the translation.) A proof of this theorem can be found in Appendix 1 of [14], as well as in many standard geometry texts. Given that every isometry is composed of one, two or three reflections, it is not hard to show that the composition of two reflections is a translation (if the reflection lines are parallel) or a rotation (about their point of intersection, if the two lines intersect), while the composition of three reflections is either a reflection or a glide reflection. These facts complete the proof. When a drawing is made in the plane there may be various (rigid) motions of the plane which take every point of the drawing onto a point of the drawing. For example, if a perfect circle is drawn with a compass, then any rotation about the center of the circle takes every point of the circle onto another point of the circle. If the drawing of footprints shown in Figure 4 extends forever to the left and right then a translation by vector 2v takes every point of one footprint to a point on another footprint. In the first case we say that the drawing "admits a rotation", or "rotation about the center of the circle is an isometry of the drawing". In the second case we say that the drawing "admits a translation", or specifically, "translation by 2v is an isometry of the drawing". In the systematic classification of patterns questions arise such as, "Is there a rotation?", or "Is there a translation?". The answer to the first question is "yes", for the circle and "no" for the footprints. The answer to the second question is "no" for the circle, and "yes" for the footprints. Another common question is "Is there a reflection?", to which the answer is "yes" for the circle (in any line through the center point of the circle), and "no" for the footprints. 2.2 Dimensionality (1, 2). Figures like the circle which do not admit any translation are called finite. Figures like the string of footprints, which admit translations in one direction (and its opposite) only are called one-dimensional, or more briefly, bands or strips. Figures like the pattern from Borneo in Figure 7 (imagined to extend to infinity in all directions) which admit translations in two directions are called two-dimensional. (Two translation vectors are marked in Figure 7. Note that if there are translations in two directions then there are translations in infinitely many directions, since the two translation vectors can be combined in infinitely many ways.) Thus dimensionality is completely determined by the nature of the translations which a figure admits. 
Figure 7: Two-dimensional
pattern showing
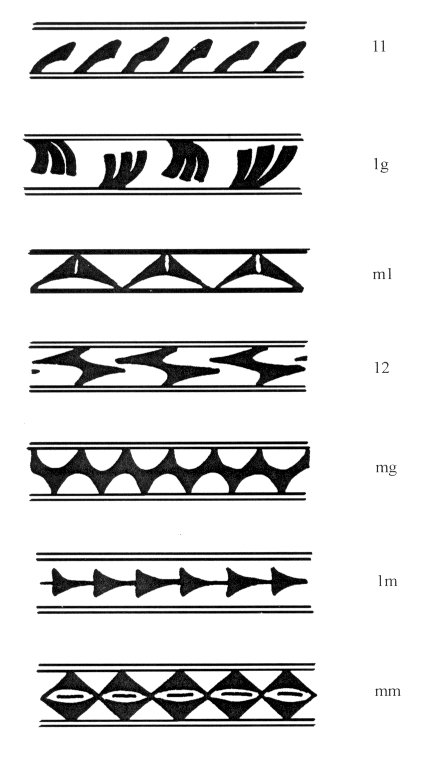
2.3. The Seven One-Dimensional Patterns. It is not very hard to see that there are a limited number of kinds of isometry which are admitted by a one-dimensional pattern. By definition, there are translations in only one direction (and its opposite). This means that if there is a glide reflection it must be in the same direction as the translations. (For, if the glide reflection were in a different direction, then applying it twice would yield a translation in that different direction - think of the footprints, where applying the glide reflection twice yields a translation by 2v in the direction of the glide reflection.) Moreover, it is not hard to see that any reflection must be in a line in the direction of the translation (which we call "horizontal" for convenience) or perpendicular to that direction (i.e. "vertical") so there can be only these two kinds of reflection. Finally, the only possible rotation is a half-turn (180o), which interchanges the translation vector with its opposite. Thus, aside from the translations (by v and its multiples) which are present in every one-dimensional pattern (by definition!) there are only four possible kinds of isometry for a one-dimensional pattern: reflection in a line parallel to v ("horizontal reflection"), reflection in lines perpendicular to v ("vertical reflection"), half-turns, and glide reflection. Note again that the phrase "horizontal reflection" is used merely as an abbreviation for "reflection in the central axis of the infinite band", and "vertical reflection" refers to reflection in a line perpendicular to the direction of the band. Each of these four may be present, or absent, in a given one-dimensional pattern. This means that there are 16 possible combinations of these four isometrics. At first it might seem that there would thus be 16 possible one-dimensional patterns. However, some short arguments (which can be found in Appendix 2 of [14] show that nine of these combinations are actually not possible. For example, suppose one tries to construct a one-dimensional pattern having a horizontal reflection, and a vertical reflection, but no half-turn. It can easily be verified that a reflection followed by another in a line at right angles to it is a half-turn. Hence the suggested combination is impossible; the presence of the two reflections guarantees the presence of a half-turn. The remaining seven combinations can actually occur. Figure 8 shows examples of all seven from the pottery of San Ildefonso pueblo [7]. A simple naming system for the one-dimensional patterns was suggested by Marjorie Senechal and has become fairly widely used, though it is certainly not the only one you will find in the literature. Each of the seven patterns has a two-symbol name, obtained as follows: The first symbol is m if there is a vertical reflection; otherwise it is 1. The second symbol is m if there is a horizontal reflection; otherwise it is g if there is a glide reflection, 2 if there is a half-turn (but no glide reflection), and 1 otherwise. It does not take long to become adept
at recognizing and labeling real-world examples of the seven one-dimensional
(strip) patterns. For practice the reader can try to verify that the San
Ildefonso patterns in Figure 8 have been labeled correctly.
Figure 8: Examples
of all seven one-dimensional patterns,
There are many cultural contexts in which all seven strip patterns occur. Examples from the Bakuba of central Africa and the old kingdom of Benin in present day Nigeria can be seen in [2,3]. However, the relative frequency of the occurrence of the various patterns in a given context varies widely. For example, in Anasazi pottery of the U. S. Southwest some 70% of the identifiable strip patterns have only half-turn symmetry and translations (type 12). This contrasts with the smoking pipes studied by the author from the site of Begho, Ghana, where nearly 70% of the strip patterns have all four of the possible strip symmetries (type mm) [4]. 2.4. The Seventeen
Two-Dimensional Patterns. We might hope that the classification
of two-dimensional patterns in the plane could proceed in the same way
as the simple classification of plane patterns, taking into account the
fact that there are more possible translations, rotations, reflections
and glide-reflections. However, at first glance there seem to be far too
many possible isometries - rotations by any one of infinitely many angles
(not just the half-turns of strip patterns), reflections in lines in almost
any combination of directions, translations and glide-reflections in all
directions. Fortunately, it is not quite that complicated (though it is
too complicated to outline briefly) because of the so-called "crystallographic
restriction".
This restriction, which is a purely
geometric one, in spite of the name, says that for any pattern which admits
translations in more than one direction the only possible rotations are
by 180o, 120o, 90o, and 60o,
that is, by a half-turn, third of a turn, quarter-turn, or a sixth of a
turn. Another way to put this is that there cannot be rotation by a fifth
of a turn, or by any turn less than 60o. You may think you have
seen pentagonal symmetry in such patterns as the one in Figure
9a, but careful examination shows that this pattern has only half-turn
rotations. Likewise, the pattern in Figure 9b may seem
to have octagonal symmetry, but in fact only has quarter-turns.
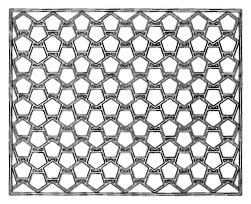
Figure 9a: This
two-dimensional pattern does not
Figure 9b: This
two-dimensional pattern does
As a consequence of the restriction on rotations the angles between lines of reflection (or glide-reflection) are also restricted (since combining two reflections in lines at a given angle yields a rotation by twice that angle). So there are not as many combinations as it might seem, though their interrelations are more complex than in the one-dimensional case. Careful analysis shows that in fact there are only 17 combinations, and hence only 17 two-dimensional patterns. A useful flowchart for identifying the type of any given repeated two-dimensional pattern is given as Figure 10. The notations are standard crystallographic symbols. 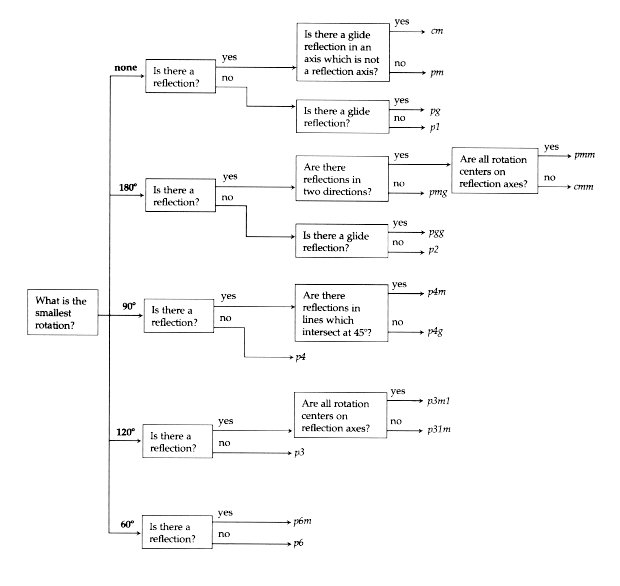
Figure 10: Flow chart for determining the type of any of the seventeen two-dimensional patterns. Unfortunately, in contrast to the one-dimensional case, there is no really simple recipe for deriving these symbols, though with use one begins to recognize some significance to the symbols. For example, a number occurring in the name indicates the presence of the corresponding rotation; the occurrence of m or g indicates the presence of reflections (m for mirror, g for glide reflection); and a c indicates a "half-drop" in the language of some designers. A glimpse of this is shown in Figure 11. There the placement of the windows (omitting the one at the very top) in the facade of the grain storage building in Torun, Poland (the birthplace of Copernicus) yields a pattern of type pm. If the windows were rectangular, thus admitting reflections in both horizontal and vertical lines, the type would be pmm. However, in the Roman tile pavement from Perge, Turkey (identified with the geometer Apollonius) the individual lozenges have mirror symmetry in only one direction, and their arrangement is by "half-drop"; thus the pattern is of type cm. Finally, the "cracked ice" pattern from China has 60o rotational symmetry (around the centers of the hexagons) but no reflections. Hence it has type p6.
Figure 11a: Granary in Torun, Poland.
Figure 11b: Roman mosaic in Perge, Turkey.
Figure 11c: Pavement pattern from China. Schematic drawings of each of the 17 are
given in Figure 12. In many cases it is possible to
identify a given pattern in the field by simply matching it with one of
the prototypes. Then the flowchart can then be used to provide a check
on the correctness of this identification. For practice the reader may
verify that the pattern of Figure 9a is of type pmg
(reflections in vertical lines, and glide reflections in horizontal lines),
while Figure 9b has type p4m, the same as an ordinary
checkerboard.
Figure 12: Schematic
representations of the seventeen two-dimensional patterns.
3. The Story of Edith Mueller. The person many of us credit with making the first significant study of patterns in a cultural context, Edith Mueller, was in fact neither a mathematician nor a crystallographer, but an astronomer. And, although her study involved the ornamental work in the Alhambra in Granada, she never lived in Granada, and never studied these ornaments in situ. Her father was a Swiss engineer who lived in Madrid. While still in high school she had been inspired by reading Sir James Jeans' The Universe Around Us to become an astrophysicist. She began her university studies at the University of Zurich in 1937, with this as her goal. However, the professor of astrophysics discouraged anyone from trying to have a career in astronomy, first because it was a very difficult subject (which he made no attempt to make easy) and second because it was very difficult to get a job in that field. She had taken a general course from Speiser in which he discussed the symmetry of ornaments as presented in his group theory book. Having grown up in Madrid, she had visited the Alhambra, so she asked Speiser whether she could prepare a paper on the Alhambra ornaments to submit for a Master's degree in mathematics in order to have some paper credentials to get a job. Speiser was "thrilled at the idea", and she returned to Madrid where she found a book with big photographs from the Alhambra. Working entirely from this book she made a detailed symmetry analysis of the Alhambra ornaments and left the resulting paper at Speiser's house for him to read. He phoned her at midnight, saying "Congratulations on your PhD thesis!'. To which she replied "Oh no, that's just the first chapter of my Master's thesis." Eventually a compromise was worked out: she would submit the paper for an immediate Master's degree (in 1943) and then add a section and complete a few courses to obtain a PhD (in 1944), with her thesis, Gruppentheoretische und Strukturanalytische Untersuchungen der Maurischen Ornamente aus der Alhambra in Grenada [11]. After this seminal work Edith Mueller taught mathematics in a girl's school in Zurich for three years. But then WWII was over and the men came back to reclaim their jobs. She got a job in the astronomical observatory in Zurich, and made contacts which led in 1952 to job offers all over the world. After ten years at the University of Michigan, she returned to Geneva in 1962 where she eventually became professor of astronomy until her retirement in 1983. She moved to Basel in 1984, and it was there that she told me her story in 1994. Although she had been invited by Dénes Nagy to attend the first conference of ISIS Symmetry in Budapest in 1989 she seemed to have little idea of the wide influence of her work. It is an interesting sidelight that M.
C. Escher contacted her in 1948 or 1949 while she was working at the observatory,
and asked to visit her in Zurich to see her thesis, about which he had
heard. Although he was more or less unknown at that time, he showed her
his portfolio of prints and gave her an original of "Air and Water" which
(in 1994) was hanging on her living room wall. This story can be added
to the arsenal of those who suspect that Escher's repeated claim to be
completely ignorant of mathematics was exaggerated for effect.
4. Field Trips to Fiji and Tonga. In real-world patterns it is not uncommon for patterns to occur which are composed of two congruent parts which are colored two different colors. In the case of finite designs the most familiar is perhaps the circular yin-yang symbol. Among two-dimensional patterns the checkerboard is a familiar example. When the idea of symmetry of pattern is extended to include color-exchanging isometries the number of patterns increases: there are 17 such two-color bands, and 46 two-color two-dimensional patterns. Since n-color patterns for n > 2 are not very common our handbook [14] was written to include only the one- and two- color patterns. While there are many two-color bands in pueblo pottery, as illustrated by the 14 found decorating the pottery of San Ildefonso [7], it is in the Pacific that two-colorings have particularly flourished. 4.1. Fiji.In Fiji the most striking examples of two-color symmetry are found in the stenciled bark cloth decorations made in Cakaudrove province on the island of Taveuni, northeast of the main island of Vitilevu where the cities of Nadi and Suva are located. Although the author had been familiar with these patterns from striking museum examples (indeed one such was chosen by the publisher to be the jacket design of [14]) he was astonished to find, during a short visit to Suva in 1990, that the craft was still alive and well. Indeed, because this island was the home of the then president of Fiji a manikin clothed in these patterns greeted the visitor to the Fiji Museum in Suva, while down the road the visitor's center was wallpapered with Cakaudrove decorated bark cloth. (See Figures 13 and 14.) I immediately began arranging for a return trip, to the source of these items, the president's home village of Somosomo, Taveuni. This was a joint project, with Dénes Nagy of ISIS-Symmetry, who was at that time teaching at the University of the South Pacific in Suva. The following paragraphs are a summary of the detailed report found in [8]. 
Figure 13: Manikin in the Fiji Museum, Suva, 1990, wearing masi kesa (Fijian stenciled bark cloth).
Figure 14: Fine
Nailevu with the bark cloth wall decorations made under her
In Somosomo we were the guests of Fine Nailevu, who was in charge of the manufacture of the cloths for the Fiji Museum manikin in Figure 13 - she is shown in Figure 14 seated in the president's Somosomo vacation house in front of the wall decorations whose stenciling she supervised. She tutored us in the process of making bark cloth, told us the names of the stencils used in the dyeing process, and stenciled two small cloths for us in the course of a Saturday morning. Figure 15 shows one step in the stenciling process, and Figure 16 shows one of the finished cloths. 
Figure 15: Fine
Nailevu working on the “waterfall”
The ultimate raw material for these decorated cloths is the paper mulberry tree. Small trees, some 2 inches in diameter, are stripped of their bark, the inner part of which is then soaked and pounded out into flat sheets several feet long and a foot or two wide. These are then felted together to make larger sheets, which can in turn be cut to sizes required for various purposes. The stencils, traditionally made from leaves, are now made from more durable X-ray film. The dye is made from soot collected from the burning nut of a candlenut tree, mixed with a solvent such as kerosene. Each individual stencil has the same name
as the repeated pattern made by applying it, with minor variations. For
example, the stencil used to make the border pattern in Figure
16 consists of four adjacent notched rectangles which is applied four
times to make the sixteen black notched rectangles along the lower edge.
It is called "interrupted waterfall", because a double row of this same
pattern (often seen on larger cloths) is simply called "waterfall", suggesting
that the version in Figure 16 is "interrupted". Notice
that if this stencil were the only one used to make this border, the white
rectangles, not being notched, would not match the black notched ones.
So a small triangular stencil is used to notch the white rectangles. It
was a wonderful discovery for us when we found that this small triangle
stencil is called "completion of the waterfall"! That is, Fine Nailevu,
and all those stencilers before her who have used this pattern for a hundred
or more years, have the same mathematical yearnings as we do. They want
to make a perfect two-color pattern, where the white part is exactly congruent
to the black.
Figure 16: The completed cloth from Figure 15. We made a count of the number of different two-color patterns found in Cakaudrove cloth in Somosomo or museum collections. There were 12 of the 17 possible two-color bands, and 12 of the 46 possible two-color two-dimensional patterns. We did not have a big enough sample to be able to say anything about the relative frequency of occurrence of the individual types. An extensive discussion, with many illustrations, of the role of bark cloth in Fijian culture has been given recently by Rod Ewins [10]. Elsewhere he has pointed out that it is important to consider not only the individual strip patterns, but their arrangement on the cloth as a whole. Thus, while the strip pattern along the central zigzag of Figure 17 is of type mg, the zigzag itself turns the overall pattern of the whole cloth into an mg strip as well. Another striking example is shown on the large cloth reproduced as the jacket of [14]. This two-dimensional pattern is composed of a number of smaller strips arranged so that the overall pattern looks like over-under weaving, of type p4g. According to Ewins, the individual Cakaudrove strip patterns are very standardized, both in space and time (museum specimens from over a century ago show virtually identical strips to those used today). However, the overall layout on whole cloths often gives a clue as to the location within Cakaudrove province where the cloth was produced. 
Figure 17: A
stenciled bark cloth showing overall
In the 1930's H. J. Woods, a scientist at the Department of Textile Industries of the University of Leeds, was the first person to publish illustrations of the 17 and 46 two-color strip and two-dimensional patterns in a form analogous to the border of Figure 16, i.e. completely filling the border (or plane in the two-dimensional case) [5]. Some of his illustrations are strikingly similar to Cakaudrove patterns, down to such detail as the small white and black horizontal bars which surround the interrupted waterfall in Figure 16. We know that the Pitt Rivers Museum in Oxford owns an old Cakaudrove cloth with a pattern much like one of the ones Woods invented, and that Woods was an undergraduate at Oxford where he would be expected to have visited the Pitt Rivers. It is an interesting speculation that these prototype mathematical drawings of Woods might have been inspired, at least subconsciously, by Cakaudrove patterns from the other side of the world. 4.2. Tonga.From museum specimens of large pieces of Tongan bark cloth, one might imagine that there is some overall symmetry to these pieces like that of the Fiji pieces just discussed. However, when it is found that these large Tongan cloths are decorated by passing them repeatedly over a table on which various pattern boards have been placed, we see that the basic overall symmetry is just that of translation. Figure 18a shows the work table across which the cloth is passed after each rubbing. In this way the designs from the pattern boards underneath the cloth on the table are copied repeatedly to obtain a decorated cloth of almost any desired length. Figure 18b shows a completed long cloth laid out to dry. 
Figure 18a: Tongan
women decorating and assembling
Figure 18b: A completed cloth like that of Figure 18a. However, there is a fascinating Tongan
craft which is not ordinarily seen in museums, that of rafter lashing,
which sometimes generates striking examples of two-color patterns. Formerly
functional, in that it bound rafters together in a flexible manner that
could withstand high winds, it is now purely decorative. It is found binding
the concrete structural posts on the property of wealthy patrons such as
churches, banks and the homes of the Tongan nobility. Several remarkable
examples are shown in Figure 19. These were all made
in 1989-90 under the supervision of one skilled artisan, Tamale of Niutoua
for the Tokaima'ananga Tongan Methodist Congregation church in Otara, New
Zealand. The bindings are made by wrapping two colors of coconut fiber
twine alternately around a cylindrical core. During the construction process
the final pattern is hardly discernible, but the end result is quite often
a perfect two-color pattern with the dark and light regions being exactly
congruent, as in Figures 19a and c.
Figure 19a, b, c: Three
rafter lashings made in 1989-90 for a Tongan church
There are other remarkable examples of two-color patterns to be found in Tonga. These include basketry works, woven trays made primarily for the tourist trade, and another style of decorative rafter lashing which was made for the opening of the Basilica of Saint Anthony of Padua in Nuku'alofa in 1980. A more extensive discussion, with photographs, is found in [6]. 4.3. Admiralty
Islands. Our final Pacific example comes from decorative bindings
of functional and ceremonial obsidian-bladed spears in the Admiralty Islands.
In the list of 46 two-color two-dimensional patterns there are exactly
five two-colorings of the particular underlying pattern pmm. Examples of
these all occur in the elaborate decorations on the spears collected between
the years 1870 and 1920 and currently found in two major collections, those
of the Field Museum in Chicago and of the Australian museum in Sydney.
There is some indication that the details of manufacture of the spears,
especially the decoration, reflect the economic and sociological changes
in the Admiralty Islands in those years. The kind of information which
can be obtained from these spears is the subject of ongoing study by Robin
Torrence. Did the decorations become more elaborate at certain times because
the ceremonial importance of the spears became more important in times
of peace? Or, after the spears had no function at all for warfare were
the designs modified to be more in line with what European collectors wanted?
Small obsidian daggers are still made for the tourist trade, in accordance
with a dictum quoted by Torrence that mass market "airport art" must be
cheap, portable, understandable, and dustable. This did not apply to such
a degree in the period 1910-1920 when most of the examples shown in Figure
20 were collected, though even from that period the ratio of the number
of daggers to spears that made their way to museum collections is much
larger than in earlier periods.
Figure 20a: Schematic pattern pmm.
Figure 20b, c: The
five ways of “two-coloring” the pattern in Figure 20a
are
For whatever reason, the five decorated spears shown in Figure 20 constitute a complete catalog of the five possible ways of two-coloring the (uncolored) prototype pmm pattern which accompanies them. This is an interesting example of the independent discovery of what might be thought of as a somewhat obscure geometric/group theoretic fact. Or perhaps we can just say that an interest in symmetry has led us to look at the Admiralty Islands with different eyes than those used by Margaret Mead in her classic Growing Up In New Guinea. More details of the history of the Admiralty
Islands and the spears can be found in [9].
References [1] G. W. Brainerd, Symmetry in primitive conventional design, American Antiquity 8(2), 164-66, 1942. [2] D. W. Crowe, The geometry of African art. Part 1. Bakuba art, Journal of Geometry 1, 169-182,1971. [3] D.W. Crowe, The geometry of African art. Part 2. A catalog of Benin patterns, Historia Mathematica 2, 253-271, 1975. [4] D.W. Crowe, The geometry of African art. Part 3. The smoking pipes of Begho, in The Geometric Vein: The Coxeter Festschrift, edited by C. Davis, B. Grünbaum, and F. A. Sherk, 177-189, New York: Springer, 1982. [5] D.W. Crowe, The mosaic patterns of H. J Woods, in Symmetry: Unifying Human Understanding, edited by 1. Hargittai, 407-411, New York:, Pergamon, 1986. [6] D.W. Crowe, Tongan symmetries, in Science of Pacific Island Peoples, Part IV, Education, Language, Patterns and Policy, edited by J. Morrison, P. Garaghty, and L. Crowl, Suva:Institute of Pacific Studies, 1994. [7] D. W. Crowe and D. K. Washburn, Groups and geometry in the ceramic art of San Ildefonso, Algebras, Groups and Geometries 3(2), 263-277, 1985. [8] D. W. Crowe and D. Nagy, Cakaudrove-style masi kesa of Fiji, Ars Textrina 18, 119-155, 1992. [9] D. W. Crowe and R. Torrence, Admiralty Islands spear decorations: A minicatalog of pmm patterns, Symmetry: Culture and Science 4(4), 385-396, 1993. [10] R. Ewins, Symmetry and semiotics: The case of Fijjian bark-cloth decoration, Embedded Symmetries, proceedings of a symposium at the Amerind Foundation, Dragoon, Arizona, April 12-17, 2000, edited by D.K. Washburn, University of New Mexico Press (to appear). [11] E. Mueller, Gruppentheoretische und Strukturanalytische Untersuchungen der Maurischen Ornamente aus der Alhambra in Granada, Ph.D. diss., University of Zürich, Rüschlikon, 1944. [12] A. O. Shepard, The Symmetry of Abstract Design with Special Reference to Ceramic Decoration, Contribution no. 47, Carnegie Institution of Washington Publications no. 574, 1948. [13] A. Speiser, Die Theorie der Gruppen endlicher Ordnung, 2 nd edition, Berlin: Springer, 1927. [14] D. K. Washburn and D. W. Crowe, Symmetries of Culture: Theory and Practice of Plane Pattern Analysis, Seattle: University of Washington Press, 1988. [15] C. Zaslavsky, Africa Counts:
Number and Pattern in African Culture, Boston: Prindle, Weber &
Schmidt, 1973.
1 This quote has been recently incorrectly attributed to Hermann Weyl.
|